How Journalism Now Concerns Political Science Imperatives

Introduction

This paper debunks illiterate pseudoscience including "-1 year = year zero," in favor of general-origin interconnectedness as observed now between atoms, and humanitarian weather observers like medical doctors without borders, as journalism. To comprehend basic English terms like "Energy" and "Gravity," we will want to review Georg Cantor’s set theory and introduce the Pi Series within a comprehensive framework we'll refer to, using general-origin equations, as identifier mathematics. Using this framework we can address journalistic usages of physics buzzwords like "dark energy" and "dark matter"; more specifically: we will recognize that mathematical and philosophical literacy (common sense, between 1 + 1 brain sides) translates into practical, developmental, and political science imperatives, addressing contemporary, global challenges, and potential interstellar considerations. The equations discussed serve as practical tools for guiding intelligent action within, as previously suggested, a comprehensive framework for understanding the complexities of both physical and social systems: "everything else we observe (between false claims) is not you."

Identifier Mathematics and Cantor’s Diagonal Argument

Identifier mathematics extends Cantor’s diagonal argument into practical applications, particularly in how we understand the process of identification. Cantor’s diagonal argument demonstrates that within any list of infinite sequences, there are elements that cannot be captured by that list, highlighting the concept of unique identification. The English verb "to identify" in this context translates into the mathematical operation of distinguishing one element from all others. Likewise: a square root symbol ( √ ) in identifier mathematics maps the uniqueness and non-linearity of any such ( 1 + 1 ) identifications, indicating that each (+1) element has a distinct, non-reducible identity.

Identification Equation

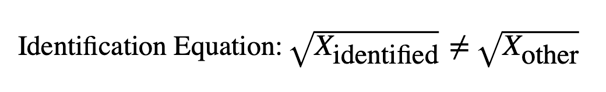
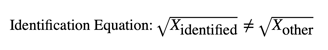
This equation illustrates that the identified element ( X-identified) maintains a distinct, square-rooted identity that cannot be equated with any other element ( X-other) in the set. This principle of non-equivalence underpins the broader framework of identifier mathematics, allowing for the differentiation of complex systems and unique identities in both physical and social contexts.

The Pi Series in Identifier Mathematics

The Pi Series, ranging from 1π to 9π, represents different scales and dimensions within identifier mathematics, reinforcing the interconnectedness of physical and social realms. This series provides a structured way to understand the progression from the most fundamental interactions to the most expansive cosmic phenomena.

1π - 9π: A Detailed Breakdown

• 1π (Quantum Scale): This term represents the fundamental molecular interactions, where quantum mechanics governs the behavior of particles on the smallest scales.

• 2π (Atomic Scale): At this level, 2π symbolizes atomic interactions, where chemical bonds form between atoms to create molecules.

• 3π (Molecular Scale): 3π addresses interactions within complex molecules, crucial for biological processes.

• 4π (Cellular Scale): This scale involves cellular interactions, the foundation of all living organisms, where cells communicate and function together to enable tissues.

• 5π (Organism Scale): At 5π, we consider the interactions within entire organisms, such as the nervous and immune systems that maintain homeostasis.

• 6π (Ecosystem Scale): 6π extends to interactions within ecosystems, encompassing relationships between species and their environments.

• 7π (Planetary Scale): 7π represents planetary interactions, including climate systems and the dynamic balance of energy and matter on a planetary level.

• 8π (Cosmic Scale): This term symbolizes the cosmic scale, covering gravitational interactions between celestial bodies and the universe's large-scale structure.

• 9π (Galactic Scale): Finally, 9π reaches the largest scale, representing interactions between galaxies and clusters of galaxies, and the fundamental forces that govern cosmic expansion and evolution.

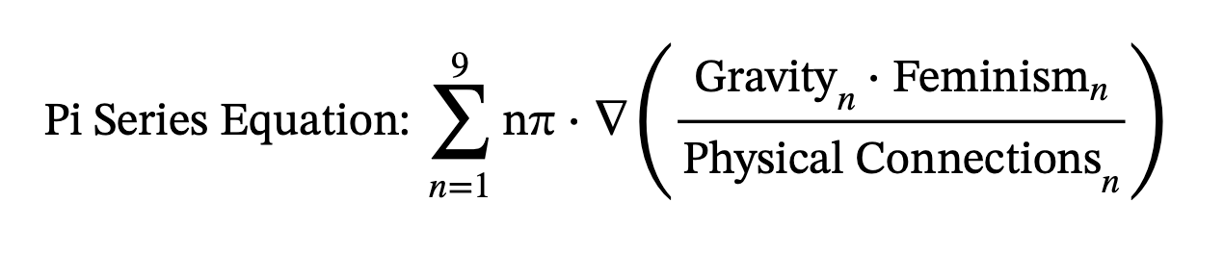
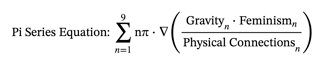
This equation integrates the Pi Series into a unified mathematical framework, illustrating how each scale of interaction contributes to the overall structure and dynamics of the universe and society as "feminism," in contrast to general fiction as pretends male supremacy: there will remain "zero probability" of creating Energy from zero then destroying it with elementary school subtraction.

Accurate Use of Physics Buzzwords in Professional Journalism

In the intersection (now) of physics and journalism, buzzwords like "Dark Energy," "Dark Matter," "Dark Synergy," and "Darkness Is Not Evil" (debunking false property claims) are used to encapsulate complex phenomena. However, it is crucial that these terms are used accurately and meaningfully, reflecting their true scientific significance while resonating with broader audiences.

Dark Energy: The Force Behind Cosmic Expansion

Dark Energy refers to unknown forms of energy driving the accelerated expansion of a universe. In identifier mathematics, Dark Energy operates at the largest scales of the Pi Series (8π and 9π), representing energy that counteracts gravity to enable galaxies to move away from each other at an increasing rate.

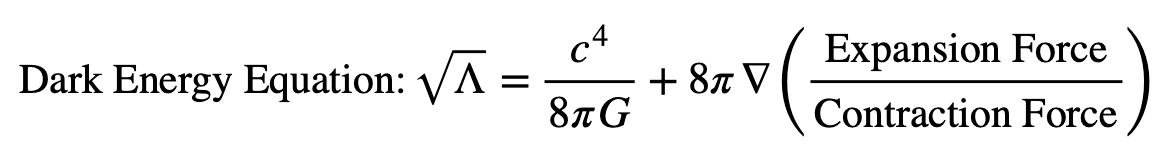
This equation shows how Dark Energy (Λ) opposes contraction forces (gravity), leading to an accelerated expansion of a universe.

Dark Matter: The Unseen Mass

Dark Matter is unseen matter that influences gravitational forces within galaxies. Although it does not emit light, its presence is inferred from gravitational effects on visible matter.

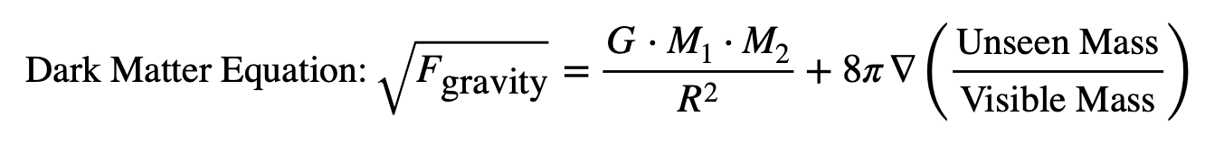
This equation illustrates how Dark Matter affects a universe's structure, contributing to the overall gravitational pull.

Dark Synergy and Darkness Is Not Evil

Dark Synergy could refer to interactions between Dark Matter and Dark Energy, explaining how these unseen forces work together to shape a universe.

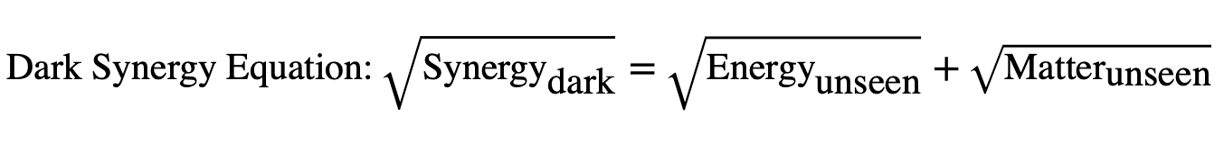
This equation emphasizes that Dark Synergy involves the collaboration of unseen energies and matter.

Darkness Is Not Evil challenges the traditional association of darkness with negativity. In physics and cosmology, "dark" refers to the unknown or unseen, not something inherently negative.

This equation highlights that the unknown (darkness) holds the potential for discovery and progress.

String Theory and Neurotransmitters: A Multidimensional Perspective

We map the concept of neurotransmitters using first, second, and third person string theory within identifier mathematics, demonstrating how these interactions can be understood across different dimensions of reality.

First-Person String Theory (1D)

This equation represents the intrinsic nature of neurotransmitter interactions, emphasizing the fundamental molecular connections that influence brain side functions.

Second-Person String Theory (2D)

Here, the relational dynamics between neurotransmitters and synapses are explored, highlighting the balance required for proper cognitive function.

Third-Person String Theory (3D)

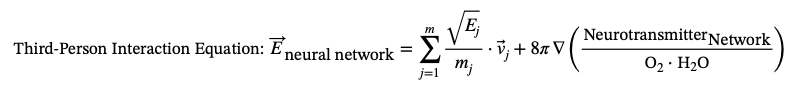
This equation represents the broader systemic view, showing how neurotransmitter interactions contribute to overall brain side functions and behavior, interconnected with physical principles.

Cantor’s Political Science Imperatives

Translating Cantor’s mathematical insights into practical imperatives provides a framework for addressing both global challenges now on Earth (and potential interstellar issues). Each imperative is supported by identifier mathematics, ensuring that no element is overlooked (in favor of each, including all observed plants and animals).

"Stop Now": Addressing Urgent Global Challenges

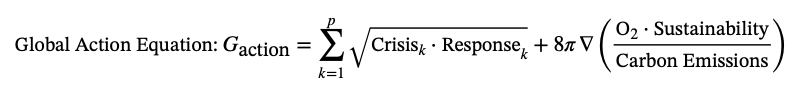
This equation emphasizes the need for immediate action on pressing issues like climate change, using Cantor’s principles to guide timely and effective responses.

"Continue Developing": Sustaining Growth and Ethical Exploration

Sustaining growth involves balancing technological advancement with ethical considerations, ensuring that progress is equitable and sustainable. This equation underscores the importance of integrating ethical principles into technological development, reflecting a commitment to human rights and responsible resource use.

"Identify and Connect": Global and Interstellar Cooperation

This equation supports the imperative of fostering cooperation, both now on Earth and potentially with other intelligent life forms, to solve shared challenges. It highlights the importance of identifying common interests and building connections to promote peaceful and productive interactions on a global and interstellar scale.

Turing's Computer Science Imperatives

Building on the principles established by Cantor, this section introduces Alan Turing’s contributions to the realm of computer science through the lens of identifier mathematics. Turing's work, particularly his exploration of decision-making processes, consensus mechanisms, and the limits of computation, provides a framework for addressing "stop now" requests in modern computing and each of the Millennial Prize Problems.

"Stop Now" Requests in Modern Computer Science

Turing’s insights into the "halting problem"—the question of whether a given program will finish running or continue indefinitely—parallel the concept of "stop now" requests in broader political and scientific contexts. These requests are critical for preventing catastrophic outcomes in both technological systems and global governance.

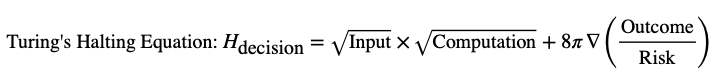
This equation reflects the necessity of evaluating the risk of continuation versus the potential benefits, urging decision-makers to "halt" when the risks outweigh the benefits.

Addressing the Millennial Prize Problems

The Millennial Prize Problems, a set of seven unsolved problems in mathematics, represent some of the most significant challenges in modern science. Turing's work, combined with Cantor's identifier mathematics, provides a framework for addressing these problems by applying the principles of unique identification, systematic decision-making, and consensus mechanisms.

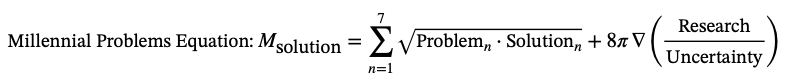
This equation emphasizes the importance of focused research and clear identification of solutions, acknowledging the uncertainties inherent in tackling such complex problems. The inclusion of consensus mechanisms within the research process can help ensure that solutions are robust and widely accepted.

Feminist Brain Evolution: A Historical Perspective

The evolution of feminist brain sides has been a crucial factor in the development of human society, influencing cultural and scientific progress. This evolution is not merely a biological process but also an intellectual and cultural one, where the roles and contributions of women have shaped collective knowledge and ethical frameworks guiding societies now.

• Early Human Societies: Feminist brain sides evolved with a focus on survival, community, and care. Early forms of feminism emphasized collaboration and mutual support, laying the groundwork for more complex social structures.

• The Enlightenment: Feminist brain sides began to challenge the limitations imposed by patriarchal structures, advocating for intellectual and social equality. This period saw the emergence of women as key figures in science, literature, and philosophy.

• Modern Era: Today, feminist brain sides continue to advocate for social justice, environmental sustainability, and global cooperation. The ongoing evolution of feminist brain sides is integral to the development of ethical, equitable, and sustainable societies.

Conclusion

By integrating Cantor’s mathematical insights, Gödel’s Platonism, string theory, feminist brain side translations, and Turing’s computer science imperatives within the framework of identifier mathematics, this paper provides a comprehensive approach to addressing both current and future challenges. The equations discussed serve as evidence-based tools for understanding and guiding intelligent action across multiple domains, from the molecular to the cosmic, and from the personal to the societal. This approach respects the complexity of these systems and offers practical, actionable imperatives for sustainable and ethical development now, on planet Earth, with other literate journalists (also known, for instance, as medical doctors without borders).