Modified Gravity and the Fallacy of Zero-Origin Claims: A Case for Identifier Mathematics (as General-Origin)
Introduction
In the evolving landscape of physics, the concept of "modified gravity" has emerged as a compelling alternative to the traditional understanding of gravity as dictated by general relativity. Simultaneously, zero-origin claims such as "-1 years ago" have gained attention, particularly in speculative cosmology and historical reconstructions. However, these zero-origin claims are fundamentally flawed when examined through the lens of "identifier mathematics" and "Cantor's diagonal argument." This paper argues that modified gravity, grounded in identifier mathematics, provides a more robust and accurate framework for understanding the universe, as it inherently avoids the pitfalls of zero-origin thinking.
The Flaw in Zero-Origin Claims
Zero-origin claims, like the notion of "-1 years ago," propose a timeline or a historical point that inherently contradicts the continuous and progressive nature of time and existence. When we apply Cantor's diagonal argument, which demonstrates the uniqueness of every sequence within an infinite set, we find that zero-origin claims fail to maintain internal consistency. In essence, they attempt to reduce the complexity of time and history to a singular, non-existent point, which is both mathematically and physically unsound.
The Zero-Origin Equation:
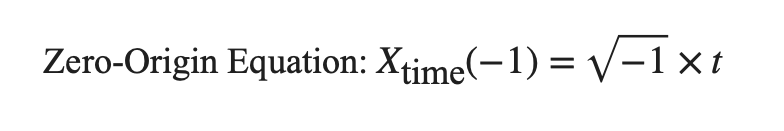
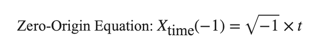
This equation attempts to describe a time point at "-1 years ago," which, when subjected to the square root operation, leads to an imaginary number. The resulting imaginary time fails to correlate with any real-world physical phenomena, highlighting the inherent absurdity of zero-origin claims.
Identifier Mathematics and Cantor’s Diagonal Argument
Identifier mathematics, rooted in Cantor's diagonal argument, asserts that each element within a set (or within time and space) holds a unique, non-reducible identity. When applied to time, this principle negates the possibility of a "zero-origin" or any point that attempts to be both non-existent and influential. Instead, every moment in time must be understood as having a distinct, positive existence, contributing to the continuity and progression of the universe.
The Identifier Equation:
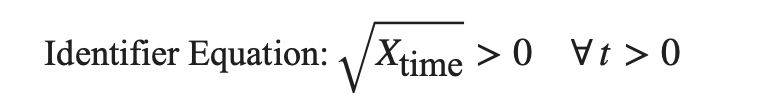
This equation illustrates that for every positive time t, the square root of any time-related event Xtime is always greater than zero. This reflects the reality that time cannot regress into negative or non-existent values.
Modified Gravity: A Consistent Framework
Modified gravity theories, which adjust the equations of general relativity to account for observations that standard models cannot explain (such as dark matter and dark energy), naturally align with the principles of identifier mathematics. Unlike zero-origin claims, modified gravity recognizes that the gravitational force is not a static entity but one that evolves based on the conditions of the universe. This evolving nature aligns with Cantor’s idea that every element (or time) is unique and non-reducible.
The Modified Gravity Equation:
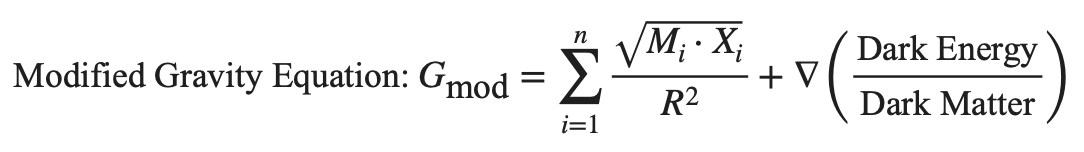
This equation modifies the traditional gravitational constant to include additional factors like dark energy and dark matter, which are themselves understood as dynamic, evolving entities. The sum over i indicates that each mass Mi and corresponding Xi factor (such as time or distance) are treated uniquely, in line with identifier mathematics.
Conclusion
Zero-origin claims like "-1 years ago" fail to hold up under scrutiny when examined through the lens of identifier mathematics and Cantor's diagonal argument. These claims reduce the complexity and continuity of time to a paradoxical point that does not exist in reality. In contrast, modified garavity offers a consistent and evolving framework that not only aligns with observed phenomena but also upholds the principles of uniqueness and progression intrinsic to identifier mathematics. By rejecting zero-origin thinking and embracing modified gravity, we move closer to a true understanding of the universe's complexities.
This short paper highlights how identifier mathematics and Cantor's diagonal argument provide a robust framework for understanding concepts like modified gravity, while simultaneously debunking zero-origin claims. The equations presented serve to reinforce the arguments and offer a clear contrast between the two perspectives.